Cavity cooling of silicon nanoparticles
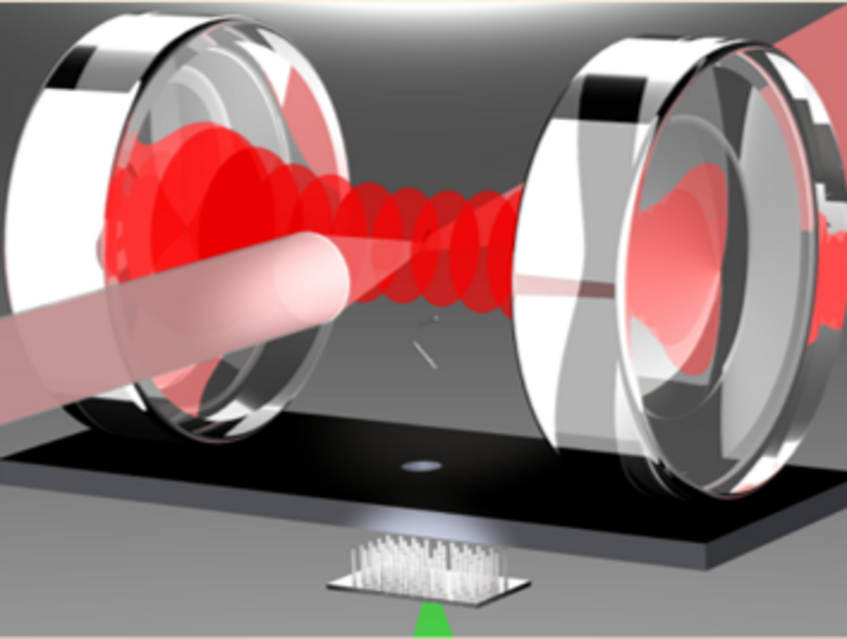
Figure 1: silicon nanoparticles are launched via laser-induced acoustic break out/break-off. The traverse a high-finesse infrared (1560 nm) cavity field. Self-induced feedback tends to extract energy from the particles and cools them.
Cavity cooling of silicon nanoparticles
What happens to a nanoparticle in strong laser light?
Intuitively one would think that in this way you just heat it up. But this answer is not always true. Since a long time, it is well known and often used in various laboratories all around the world, that laser light can be used to cool the motion of atoms. In this way, different sorts of atoms can be prepared in very cold motional states. Laser cooling has opened a still growing and very successful field of science. Many research groups have used these methods to prepare atoms in states, which can then only be described in a quantum mechanical framework.
Performing similar quantum experiments with macroscopic and biological systems is the main focus in our group [1]. Various matter-wave interferometers [Far-field diffraction [2], KDTL interferometry [3] and OTIMA interferometry] provide a way to observe the quantum nature of increasingly massive systems, currently in the mass range of up to 10,000 amu (810 atoms per molecule). Future experiments aim at showing quantum effects with substantially more massive objects, eventually in the range of 107 ...1010 amu. This mass regime shall enable us to ...
- …explore the limits of quantum mechanics, and e.g. spontaneous localization theories.
- …address the conflict between general relativity and quantum mechanics.
- …perform quantum metrology experiments to measure properties of complex nanoparticles.
- … set up quantum experiments with bionanomatter.
All these experiments will require long interaction and coherence times of material objects in an interferometer. Therefore, a source for slow particles or (bio)molecules will be needed.
For these objects it is important to develop new laser cooling techniques since all established schemes were based on particular internal atomic properties.
They rely on the near-resonant, cyclic coupling between laser light and the internal states of the atoms. In case of nanoparticles or complex molecules, these transitions can no longer be individually resolved and resonant laser cooling methods fail.
Cavity Cooling is the solution
More than 15 years ago, Helmut Ritsch [4], a theorist from the University of Innsbruck, and his group and subsequently also the Nobel laureate Steven Chu [5] at Stanford University and Vladan Vuletic (today MIT Cambridge) formulated ideas how to circumvent this problem. One should no longer rely on the internal structure of the atoms but rather modify the properties of the light-field. The resonance of the atomic transitions can be effectively replaced by the resonance of an optical resonator (cavity).
A cavity can - in the simplest case - be considered as two opposed mirrors with a certain distance which needs to be an integer multiple of half the input laser wavelength. When the cavity is filled with laser light, a standing light wave is formed. This is a sinusoidal pattern of bright and dark regions between the mirrors. A nanoparticle that flies through this pattern always feels an attractive force towards the bright spots.
The trick of cavity cooling now is the following: A nanoparticle that moves over the standing wave effectively alters the distance between the mirrors because the light needs a longer time to travel through it (index of refraction > 1). In this way, dependent on the position of the particle, it allows more or less light to enter the cavity. By choosing the right experimental parameters, the overall cavity intensity will then always be highest whenever the particle leaves a bright region of the standing wave and will be lowest when the particle approaches it. In this way it always feels a stronger slowing force than an accelerating one.
One can imagine a ball running over the valleys and hills of a mountainous region. While travelling along the optcial landscape the particle alters the steepness of its environment by its own motion. As illustrated in the simulation below, it therefore always has to climb higher than it runs down again. In this way some of its kinetic energy is transferred to the cavity light field and overall the particle is slowed.
Experimental realization
This effect has been recently seen for the first time with nanoparticles in two independent experiments in the Vienna quantum group.
In the team of Markus Aspelmeyer, Nikolai Kiesel, Florian Blaser and colleagues realised cavity cooling of the centre of mass motion of a silica sphere, which is levitated inside the cavity [6]. The trapping mechanism in their case is aided by a dilute background gas.
In our experiment, we are able to observe cavity cooling of pure silicon nanoparticles, which are created under high vacuum conditions and which are slowed while they are freely propagating through the cavity [7]. The experimental setup is depicted in Figure 1.

Figure 2: Picture of a typical silicon nanoparticle taken under the scanning electron microscope (SEM).
The silicon nanoparticles are created and launched from below the cavity under high-vacuum conditions. We shoot at the back-side of a thin piece of silicon with a strong, laser pulse. As a result, small pieces of silicon (see Figure 2) are created on the front-side and they are launched through the cavity at low velocities (< 1 m/s). In this way, the particles have enough time to interact with the light inside the cavity.
We track the particle motion as we measure the light they scatter out of the cavity. The following animation shows the scattered light from a particle that runs over the standing wave. It demonstrates how this signal can be used to determine the particle velocity.
The Gaussian envelope of the scattered light is related to the particle crossing the cavity light field in upward direction. The fast oscillations correspond to their motion over the standing wave. In this way, both the forward as well as the transverse velocity of the particle can be measured.
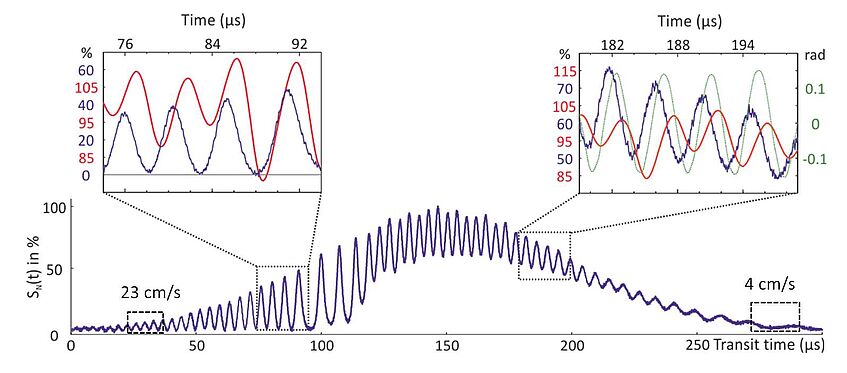
Additionally, we are able to record the dynamics of the cavity light and thus get a full inside into the cooling process. In Figure 3, these measured signals are depicted for one silicon nanoparticle. They reveal the entry and exit velocity of the particle along the cavity axis as well as the dynamics of the cavity light field. The analysis of the data allows us to conclude that:
We've shown that cavity cooling yields a reduction of the particle’s transverse kinetic energy by more than a factor 30!
The cooling of this particle can also be seen in the following animation, which is based on the experimentally measured signals.
Optical cooling of a silicon nanoparticle in transit through the intra-cavity standing light wave
References
[1] T. Juffmann, H. Ulbricht, and M. Arndt
Experimental methods of molecular matter-wave optics
Rep. Prog. Phys. 76 086402 (2013)
[2] M. Arndt, O. Nairz, J. Voss-Andreae, C. Keller, G. van der Zouw and A. Zeilinger
Wave-particle duality of C60 molecules
Nature 410, 680-682 (1999)
[3] S. Eibenberger, S. Gerlich, M. Arndt, M. Mayor and J. Tüxen
Matter-wave interference with particles selected from a molecular library with masses exceeding 10 000 amu
Phys.Chem. Chem. Phys. 15, 14696 (2013)
[4] P. Horak, G. Hechenblaikner, K. M. Gheri, H. Stecher & H. Ritsch
Cavity-induced atom cooling in the strong coupling regime.
Phys. Rev. Lett. 79, 4974–4977 (1997)
[5] V. Vuletic & S. Chu
Laser cooling of atoms, ions, or molecules by coherent scattering.
Phys. Rev. Lett. 84, 3787–3790 (2000)
[6] N. Kiesel, F. Blaser, U. Delic, D. Grass, R. Kaltenbaek, M. Aspelmeyer
Cavity cooling of an optically levitated nanoparticle.
Proc. Natl. Acad. Sci. USA 110, 14180 (2013)
[7] P. Asenbaum, S. Kuhn, S. Nimmrichter, U. Sezer, M. Arndt
Cavity cooling of free silicon nanoparticles in high-vacuum
Nature Communications 4, 2743 (2013)
[8] P. Haslinger, N. Dörre, P. Geyer, J. Rodewald, S. Nimmrichter & M. Arndt
A universal matter-wave interferometer with optical ionization gratings in the time domain,
Nature Physics 9, 144–148 (2013)
