The Talbot Effect
The Talbot Effect
The coherent, lensless self-imaging of light fields was discovered by Henry Fox Talbot in 1936[1]:
When a plane monochromatic wave illuminates a spatially periodic structure, the transmission function of this grating is reproduced as a light-field pattern further downstream, even without any imaging optics.
This phenomenon is a direct consequence of the wave nature of light but not limited to the optical domain.
It has gained technological relevance in all fields where refractive and reflective optics is a challenge, such as X-ray imaging or in particular also matter-wave imaging.
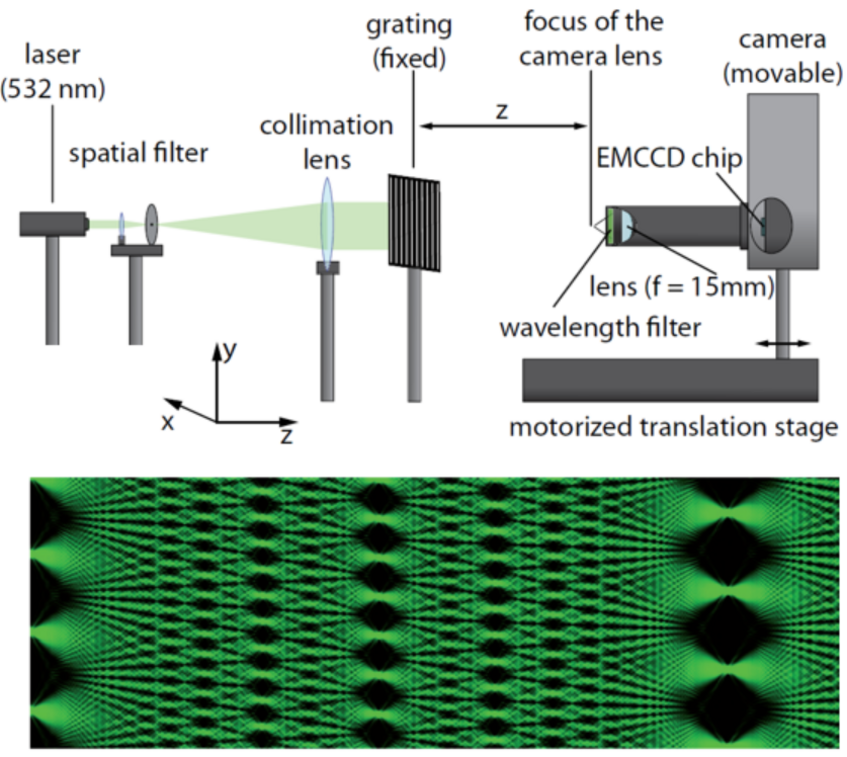
The idea behind the experiments can be easily demonstrated in a low-cost high-school experiment, illustrated in Figure 1: an expanded parallel, monochromatic laser beam is directed from left to rigth and hits a chromium plated glass grating with a period of 200 µm. The transmitted field distribution can be collected by a lens and a web cam. When this detector arrangement is displaced longitudinally, the web cam image retrieves the Talbot Carpet shown in green.
You can follow the self-imaging which occurs at multiples of the Talbot-length, L=d2/λ.
- W.H.F. Talbot, Facts Relating to Optical Science, Philos. Mag. 9, 401-407 (1836).
- K. Patorski, Self-Imaging and its Applications, in: E. Wolf (Ed.) Progress in Optics {XXVII}, Elsevier, p 2-108 (1989)
- W.B. Case, M. Tomandl, S. Deachapunya, M. Arndt, Realization of optical carpets in the Talbot and Talbot-Lau configurations, Opt. Express 17, 20966-20974 (2009).
The Talbot-Lau Effect
The Talbot-Lau Effect
Not all light sources exhibit sufficient spatial coherence to allow observing the Talbot-Effect.
Coherence can, however, be established by virtue of single-slit diffraction in an array illuminator, as first discussed by E. Lau in 1948 [1]
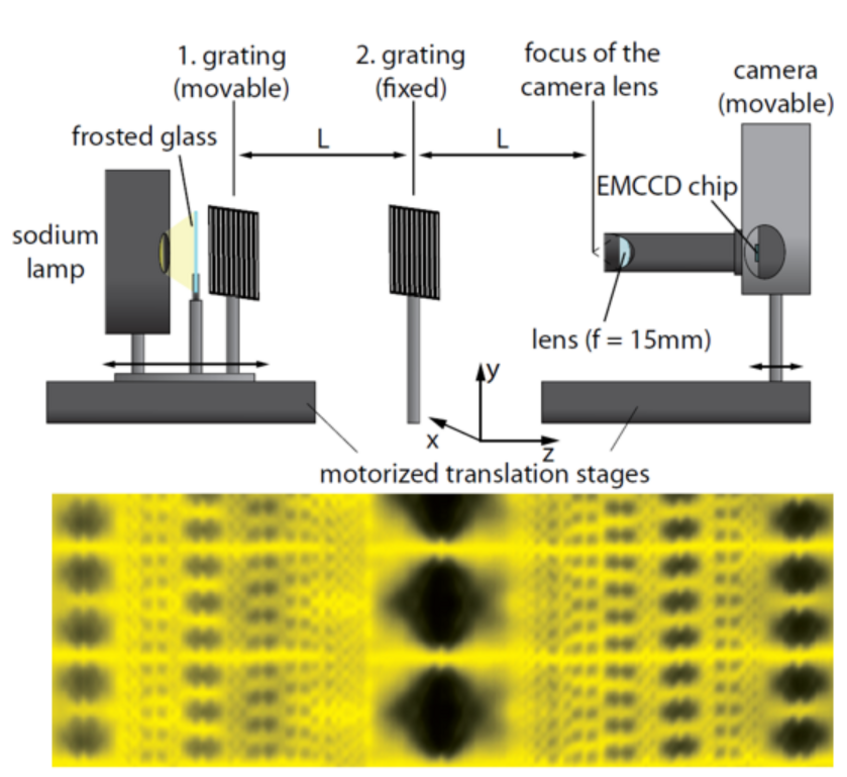
In this arrangement it is sufficient to use a relatively well monochromatic wave without initial spatial coherence. In a high-school experiment this may, for instance, be a simple sodium lamp.
While a single grating prepares coherence, it does not yet produce a intensity pattern on a screen.
This can be established by adding a second grating, at a multiple of the Talbot distance and the detector symmetrically in the same distance further downstream.
Again, self-imaging can be observed. This trick, first proposed for matter-waves by John Clauser [2] has become the basis for all near-field matter-wave interferometers run by the QNP group at the University of Vienna[3-5].
It has also gained recent technological relevance in other fields where refractive and reflective optics is a challenge, such as X-ray imaging[6].
- E. Lau, Beugungserscheinungen an Doppelrastern, Ann. Phys. 6, 417 (1948).
- W.B. Case, M. Tomandl, S. Deachapunya, M. Arndt, Realization of optical carpets in the Talbot and Talbot-Lau configurations, Opt. Express 17, 20966-20974 (2009).
- B. Brezger, L. Hackermüller, S. Uttenthaler, J. Petschinka, M. Arndt, A. Zeilinger, Matter-Wave Interferometer for Large Molecules, Phys. Rev. Lett. 88, 100404 (2002).
- S. Gerlich, L. Hackermüller, K. Hornberger, A. Stibor, H. Ulbricht, M. Gring, F. Goldfarb, T. Savas, M. Müri, M. Mayor, M. Arndt, A Kapitza-Dirac-Talbot-Lau interferometer for highly polarizable molecules, Nature Physics 3, 711-715 (2007).
- P. Haslinger, N. Dörre, P. Geyer, J. Rodewald, S. Nimmrichter, M. Arndt, A universal matter-wave interferometer with optical ionization gratings in the time domain, Nature Physics 9, 144–148 (2013).
- F. Pfeiffer, M. Bech, O. Bunk, P. Kraft, E.F. Eikenberry, C. Bronnimann, C. Grunzweig, C. David, Hard-X-ray dark-field imaging using a grating interferometer, Nature Materials 7, 134 (2008).
