Organic clusters in OTIMA interferometry
OTIMA interferometry is a universal concept that can be applied to a variety of complex molecules and even atomic or molecular clusters [1,2]. Here we illustrate it with cold clusters of anthracene, caffeine, vanilli and other organic materials. They are evaporated and co-expanded with noble seed gas from an Even-Lavie source. In this process clusters with up to 15 molecules are formed and sent towards the interferometer chamber. The cluster beam is depleted in the three optical VUV gratings of the OTIMA interferometer and analyzed in time-of-flight mass spectrometry.
The interferometer can be operated in a symmetric, balanced or "resonant" mode - when the pulse separatime times between two subsequent optical gratings are equal to within one nanosecond - or in an asymmetric, unbalanced or "non-resonant" mode, where one pair of pulses is split by an additional 200 ns. Quantum interference is expected to enhance the interferometer transmission only in the symmetric case and for cluster masses m that coincide with a multiple of the Talbot resonance T=d2m/h. Here d=79 nm is the grating period and T the pulse separation time between two subsequent grating laser pulses.
While OTIMA interferometry is non-dispersive and phase shifts do not a priori depend on the particle velocity, the molecular speed still has to be matched with the pulse separation time within some limits, to make sure all clusters are hit by the same grating at the same time. This matching is constrained by the particle velocity and the mirror geometry. The particle velocity, in turn, is determined by the pressure, temperature and mass of the noble seed gas, which entrains the molecular clusters. We can vary it for instance by changing the seed gas from argon (m=40 amu) to neon (m=20 amu). This shifts the most probably speed from 690 to 925 m/s - for all clusters, indepdent of their mass. The pulse separation time was fixed at 25.9 µs (Argon) and to 18.9 µs (Neon), respectively.
Because of the narrow velocity velocity distribution one can also picture the mass distribution to encode a distribution of de Broglie wavelengths. For any chosen grating pulse-separation time, only a narrow mass distribution will match the Talbot resonance and thus be seen with higher transmission in the detector.
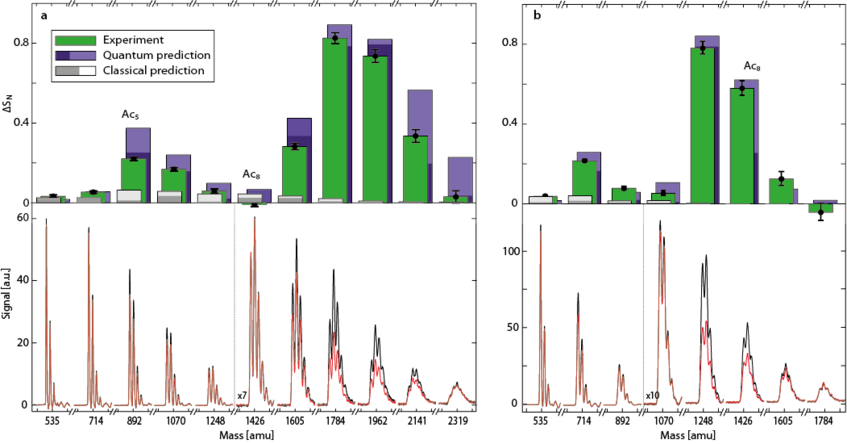
Figure 1: OTIMA experiment with anthracene clusters seeded in slow Argon (left panels) and faster Neon gas (right panels). The lower panels show the mass spectra in the resonant and non-resonant laser pulse-separation mode, from which we extract the normalized signal difference as a measure for interference contrast (upper panels). Green bars: Experiment. Purple bars: Quantum theory. Grey bars: Classcial theory. The experiment clearly supports the hypothesis that even clusters composed of a dozen weakly (van der Waals) bound organic molecules must be regarded as quantum-delocalized de Broglie waves that can be diffracted by measurement-induced photo-depletion gratings [1].
Visualizing matter-wave interference in the mass spectrum
The left panel of Figure 1 shows a Talbot mass spectrum of anthracene clusters seeded in Argon. It peaks at the decamer (10 molecules per clusters). Theory predicts and we find that changing the seed gas to Neon (and shortening the laser pulse separation time accordingly) causes the Talbot resonance to shift to lower mass, here to the anthracene octamer Ac8 (right panel).
The normalized difference between the cluster transmission in "resonant" and "non-resonant mode" is shown as green bars and compared to a simulation shown in purple. The overall structure of the mass transmission curve is very well reproduced and consistent with the assumption that even complex van der Waals clusters composed of large warm molecules must be treated as delocalized de Broglie waves.
We attribute the remaining discrepancies between theory and experiment to uncertainties in our knowledge about the molecular cluster properties, such as their optical polarizability and ionization cross section at 157.6 nm. It even appears, that OTIMA interferometry has not only been the first but that it may even be among the best existing methods to provide such numbers on VUV optical properties of clusters and molecules.
A direct comparison of the experiment with quantum and classical predictions (gray bars) also shows that assuming the quantum wave nature of the molecular clusters is a necessary requirement for a proper understanding of the experiments.
We finally note that Talbot resonance are a phenomenon recurring in time and therefore also in cluster mass at given time. Second order Talbot resonances are manifest in the transmission peak arund the anthracen pentamer (Ac5, left side, Argon seeded) and the tetramer (Ac 4, right side, Neon seeded).
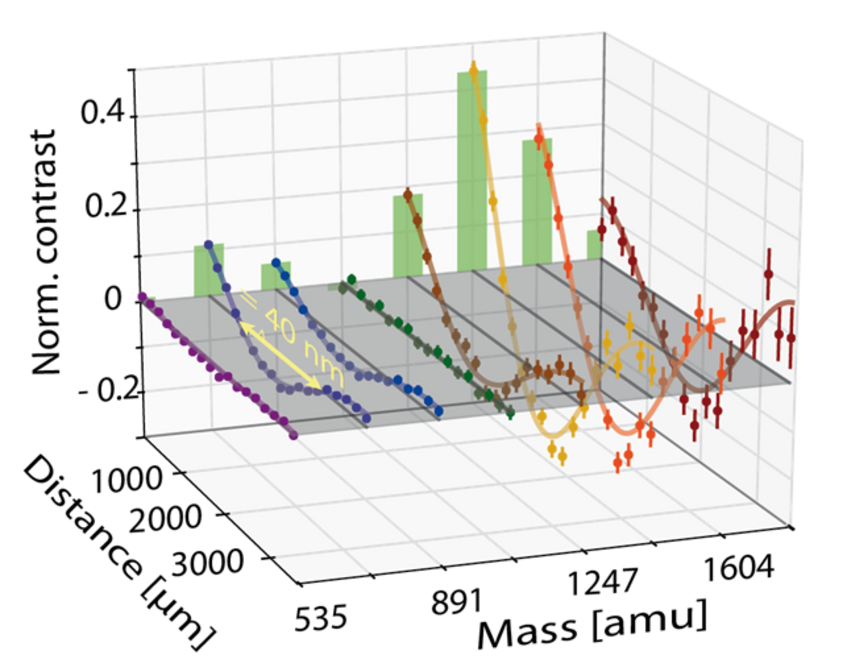
Figure 2: Cluster interference visualized in real space: we show the normalized interference contrast as a function of the shift of G2 for selected masses [1].
Visualizing matter-wave interference in real space
While the mass spectra already provide unambiguous evidence for quantum interference of molecular clusters, it is also desirable to image the interference pattern in real space. This can be done by tracing the transmitted cluster signal as a function of the position of one of the gratings. Since all gratings have the same periodicity as the interference pattern, shifting one of them will periodically modulate the particle flux behind the interferometer. For experimental reasons, we shift G2 rather than G3, by slightly tilting the laser beam and lifting the laser mirror.
Each line in Figure 2 represents the transmission of a specific cluster mass as a function of the effective grating shift. A strong sinusoidal modulation of the flux occurs only for clusters matching the Talbot resonance, in agreement with theoretical expectations.
References
[1] Haslinger P., Dörre N., Geyer P., Rodewald J., Nimmrichter S., Arndt M.
A universal matter-wave interferometer with optical ionization gratings in the time domain
Nat. Phys. 9, 144 (2013).
