OTIMA Setup: Optical TIme domain MAtter-wave interferometer
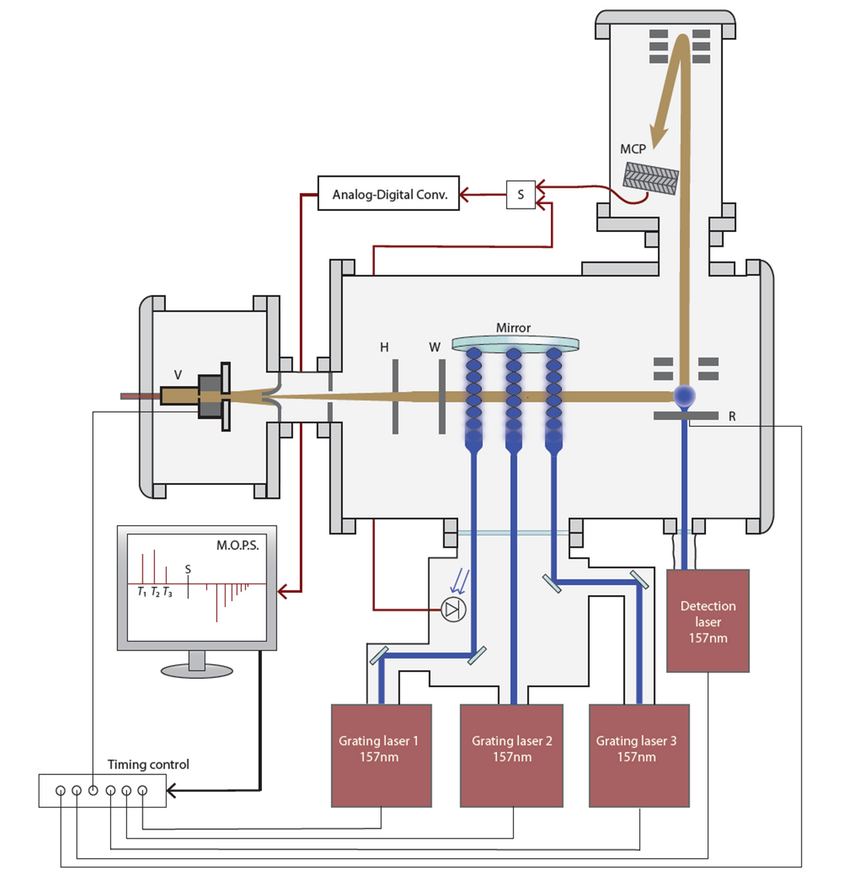
Figure 1: Experimental setup of OTIMA [1]. A supersonic expansion provides a beam of cold clusters of molecules. Three nanosecond pulsed vacuum ultraviolet laser beams form the three standing light wave gratings of the Talbot-Lau interferometer in the time domain.
OTIMA Setup: Optical TIme domain MAtter-wave interferometer
The OTIMA interferometer is a Talbot-Lau interferometer with three optical depletion gratings in the time-domain. The setup is depicted in Figure 1. A pulsed molecular source [2], emits clouds of molecules that may aggregate to large van der Waals clusters. They travel through a differential pumping stage, where the beam is shaped by a skimmer and collimated by two slits further downstream. Behind the interferometer the particles are post-ionized by vacuum ultraviolet (VUV) laser ligth and counted in time-of-flight mass spectroscopy.
The particular strength of this scheme is the use of optical VUV gratings. The laser pulses are reflected at normal incidence at a super polished mirror to form standing waves in which bright and dark regions alternate at half the laser wavelength. We use light with a wavelength of 157 nm which is invisible to the human eye. This has two advantages: it allows us to form the probably smallest conceivable free-standing grating structure and each photon in the beam has sufficient energy to realize a photo-depletion grating.
Single-photon molecular beam depletion as matter-wave beam splitter
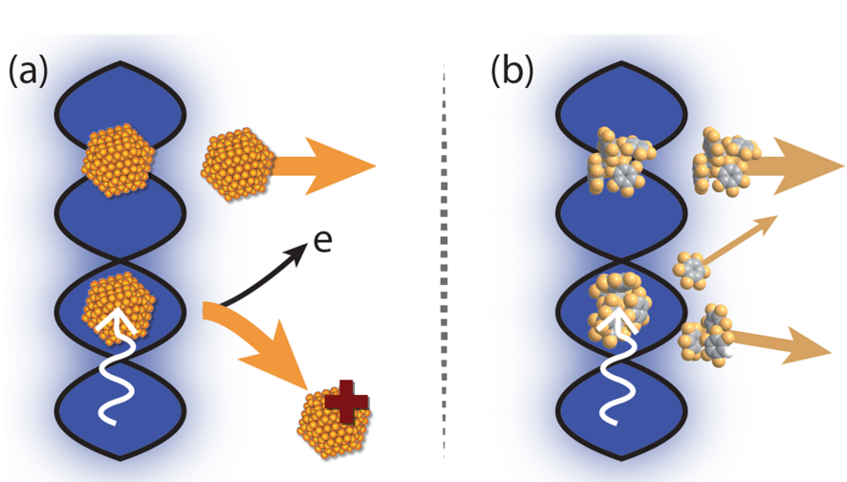
Figure 2: Photodepletion gratings realized by single-photon absorption in the anti-nodes of a light grating, where the molecule (a) ionizes and (b) fragments after the absorption of a photon [3].
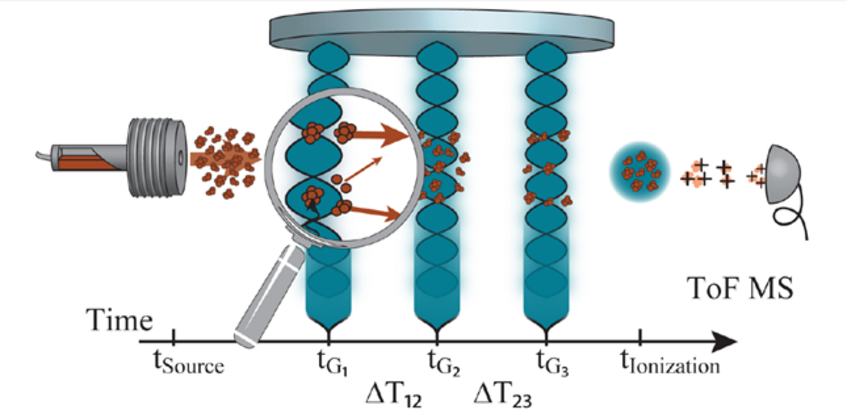
Figure 3: Talbot-Lau-interferometer OTIMA with three pulsed standing laser waves [4].
Single-photon molecular beam depletion as matter-wave beam splitter
In the anti-nodes of the light grating particles can be ionized, while particles in the nodes are unaffected. The light wave thus becomes a spatially periodic transmission filter or grating for neutral particles. Photo-depletion can be based on a variety of mechanisms that modulate the intensity of the molecular beam, for example also fragmentation, as illustrated in Figure 2. The dipole interaction between the particles and the laser light imprints an additional, spatially dependent phase onto the matter waves.
The first grating G1 thus acts as a spatial mask which prepares transverse coherence of the molecular beam by slicing it into elementary wavelets. Each wavelet develops sufficient transverse coherence during its travel to cover two or more anti-nodes of the second grating G2 to with a well-defined phase relation. The second grating acts as a combination of an absorptive and a phase grating, removing particles from the anti-nodes and imprinting a phase onto the transmitted particles. This leads to the formation of a spatially periodic intensity pattern further downstream whose period equals that of the other two gratings. The third grating G3 acts again as absorptive grating to scan the resulting interferogram.
The pulsed grating interacts with the particles at fixed time, but not at fixed position and even over 10 mm in length particles can be subjected to the same laser pulse, with nanosecond timing accuracy. Interference then occurs at a characteristic recurrence time. The first recurrence period is called the Talbot-time TT. It is determined by the particle mass m and the grating period d: TT = md2/h.
When the delays between G1 and G2 as well as between G2 and G3 are equal to the Talbot-time, the interference pattern has the same periodicity as the third grating. When the absorptive (transparent) regions of G3 overlap with the maxima (minima) of the interference pattern the number of transmitted particles is minimized (maximized). Only particles with the right mass and de Broglie wavelength show maximal modulation close to the Talbot time.
While a spatial scan of the interference pattern is possible (see [1]) we have also used different modes to detect the interference signal. Mode 1 and 2 differ in the time-delay between the laser pulses that form G2 and G3. In the "resonant" mode the pulse separation equals the Talbot-time where we expect to see interference, while it differs by 200 ns in the "off-resonant" mode, where we expect no effect. The normalized difference of the signals recorded in these two modes is then proportional to the theoretical visibility V [5].
References
- Haslinger P., Dörre N., Geyer P., Rodewald J., Nimmrichter S., Arndt M.
A universal matter-wave interferometer with optical ionization gratings in the time domain
Nat. Phys. 9, 144 (2013). - Even U., Jortner J., Noy D., Lavie N., Cossart-Magos C.
Cooling of large molecules below 1 K and He clusters formation
J. Chem. Phys. 112, 8068-8071 (2000). - Dörre N.
Time-domain matter-wave interferometry with clusters and large molecules
Dissertation, Univ. Vienna (2015). - Dörre N., Rodewald J., Geyer P., von Issendorff B., Haslinger P., Arndt M.
Photofragmentation Beam Splitters for Matter-Wave Interferometry
Phys. Rev. Letters 113, 233001 (2014). - Nimmrichter S., Haslinger P., Hornberger K., Arndt M.
Concept of an ionizing time-domain matter-wave interferometer
New Jour. of Physics 13, 075002 (2011). - E. Reiger, L. Hackermüller, M. Berninger, M. Arndt,
Exploration of gold nanoparticle beams for matter wave interferometry,
Opt. Commun. 264, 326-332 (2006).
