Quantum Soccer Ball
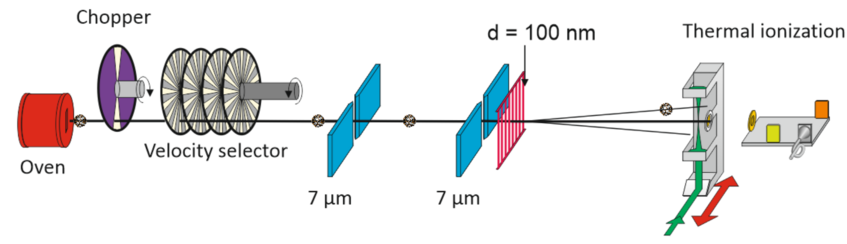
In 1999, molecular diffraction of the fullerene C60 at a nanomechanical grating showed for the first time that not only light, electrons, neutrons or atoms but also massive composite systems can follow de Broglie’s wave idea, even when they are heated to 900 K and can therefore be treated as classical thermal bodies in their internal degrees of freedom [1].
Why fullerenes?
Fullerenes are covalently bound carbon clusters. C60 is composed of 60 carbon atoms arranged in the shape of a soccer ball with a total mass of 720 amu and 174 vibrational degrees of freedom. Its larger brother, C70 contains 10 additional carbon atoms and resembles rather a rugby ball. Fullerenes were excellent candidates for a start, since they are extremely stable even at the high temperature required to make an intense beam and they can be laser-ionized and counted background free in high vacuum even without the need for mass spectrometry.
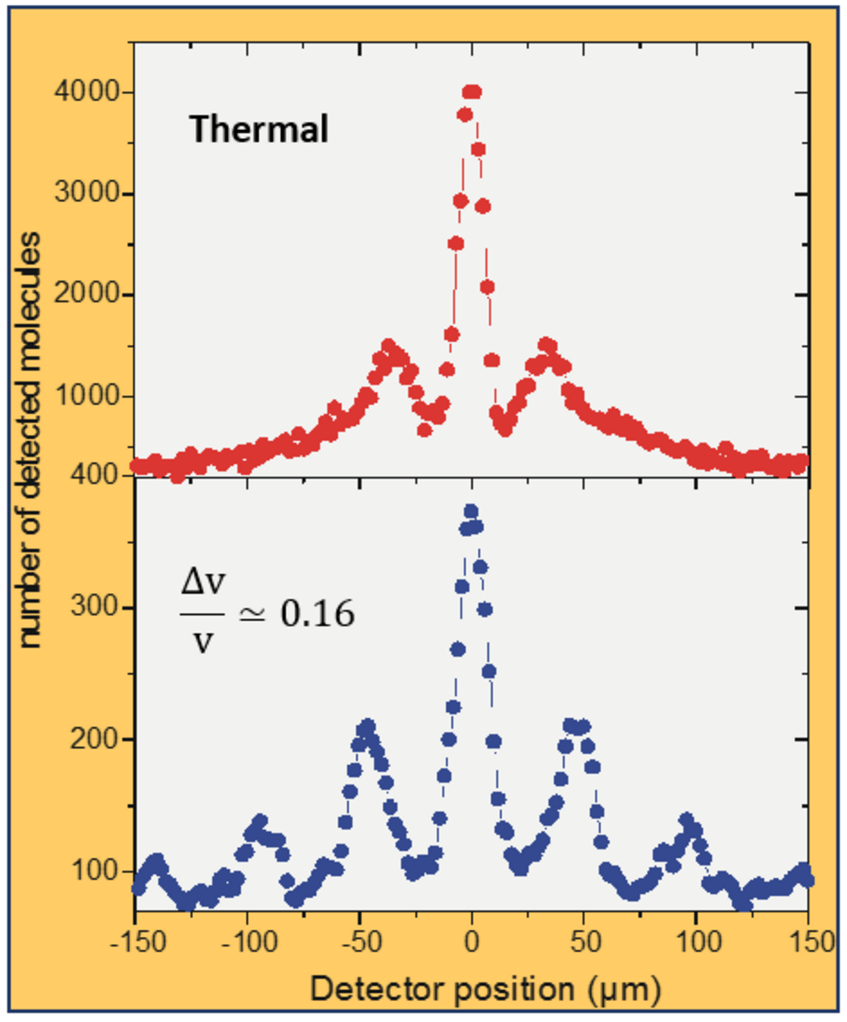
Top: In a thermal fullerene beam the velocity spready amounts to a about 60% of the central velocity. The longitudinal coherence therefore suffices only to generate first order diffraction fringes.
Bottom: using a slotted disk velocity selector one can reduce the velocity spread to only 1/6 of the central speed. This allows to observe higher diffraction orders, as well.
Source
The C60 molecules were evaporated in an oven at about 900 K, reaching velocities between 100-200 m/s and de Broglie wavelengths between 3-6 pm. The initial thermal coherence amounts is of the same order - both longitudinally and transversally and still too small for any measurable quantum
Coherence & Heisenberg’s Uncertainty
A key to this experiment is the preparation of transverse coherence: the molecules have to be delocalized over at least two neighboring slits at the grating. This can be realized using Heisenberg’s uncertainty relation: Δx⋅Δp ≥ h.
When a molecule passes the first collimation slit, this prepares a position uncertainty of the same witdth Δx. If the slit width is on the order of tens of micrometer, the final molecular beam width is a classical shadow of the slit. When the slit width is gradually reduces the uncertainty relation starts playing a role and the transverse momentum p of the passing molecules is less and less well defined [2]. For molecules with a de Broglie wavelength of the order of a few picometers the angle uncertainty amounts to a few microradian if the slit width shrinks to a few micrometers or less. Decreasing the slit width then widens the signal at the detector: a better confinement (small Δx) results in stronger delocalization (large Δp).
From delocalization to diffraction
The particle beam was collimated to 10 µrad using two slits and the molecules were diffracted at a free-standing 160 nm thick silicon nitride grating with a period of 100 nm and a slit opening of 50 nm. In a thermal beam the longitudinal coherence does not even reach two de Broglie wavelengths and the diffraction pattern only shows one clear diffraction side peak on each side of the central maximum.
Ion detection by thermal emission of electrons
After another 1.25 m of free flight the molecular density pattern was detected by laser-induced ionization. An intense argon-ion laser beam was focused down to 8 µm and aligned parallel to the grating bars. Molecules entering the laser beam absorbed several photons, were heated, ionized and counted. Scanning the laser beam across the interference fringes allowed detecting the entire diffraction pattern. The capability of thermionic emission is a specific quality of fullerenes: even when heated to several thousand Kelvin they would preferentially cool by blackbody radiation or electron emission than by fragmentation (C2-emission). In this regard a fullerene molecule resembles the hot tungsten wire of a incandescent light bulb.
Matter-wave interferometry is single-particle interferometry
Like every particle in any matter-wave interferometers each molecule only interferes with itself. In macromolecule experiments this is particularly intuitive since the chances of two molecules to be indistinguishable in all internal states (electronic, vibrational, rotational, hyperfine, Zeeman, configuration...) are vanishingly small.
References
- M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw, A. Zeilinger,
Wave-particle duality of C60 molecules.,
Nature 401, 680-682 (1999) - O. Nairz, M. Arndt, A. Zeilinger,
Quantum interference experiments with large molecules,
Am. J. Phys. 71, 319-325 (2003). - O. Nairz, M. Arndt, and A. Zeilinger,
Experimental Verification of the Heisenberg Uncertainty Principle for Fullerene Molecules.
Phys. Rev. A 65, 032109 (2002) - M. Arndt, O. Nairz, J. Petschinka, A. Zeilinger,
High contrast interference with C-60 and C-70,
Comptes Rendus De L Academie Des Sciences Serie IV 2, 581-585 (2001). - O. Nairz, M. Arndt, A. Zeilinger,
Experimental challenges in fullerene interferometry,
Journal of Modern Optics 47, 2811-2821 (2000).
